
FORMULAS
It is often important to know how to obtain a certain unknown number from other numbers which are known. The value of the number which we want to find depends upon the values of the known numbers. Thus the area of a rectangle depends upon the values of two numbers, the length and the width. The relation between the area and these two numbers is definitely stated by the formula A = lw.
There are many ways of expressing relationship between numbers. In arithmetic it is usually expressed by a rule stated in words; by using the language of algebra we, abbreviate these rules into formulas. When we try to get-the formula corresponding to a word statement, we may write the words on a single line and then place directly beneath each word or phrase the algebraic symbol that has the same meaning:
Example 1
The perimeter of a square is four times the side, P=4 × S or P=4S
Example 2
The surface 5 of a square box is equal to the sum of twice the S=2, square of its length l and four times the product of the length and the depth: l2+4×lh or S=2l2+4lh.
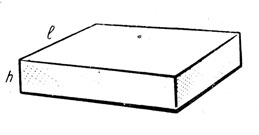
Рисунок. Расчет площади
The most common relations between numbers are obtained by the four fundamental operations: addition, subtraction, multiplication and division.
Numbers and Quantities
Letters in algebra are used to represent numbers, not numbers-of-things.
A letter may stand for 2, 15, ? etc., but not for 2 pence, 15 days, ? mile, etc.
A number-of-things is called a quantity. When you deal with quantities, always state what the unit is, as in the following examples:
A parcel weighs Wlb.; a book costs С shillings; a room is H feet high.
Note: lb. - сокращенное от латинского libra - фунт. По-английски вместо lb. читаем pound.
The Use of Symbols
The symbols +, -, ×: have the same meanings in algebra as in arithmetic.
The following symbols are in common use:
= means is equal to or equals; thus 5 - 2 = 3 and 4 × 5=20.
∴means therefore; thus 1 yd. = 3ft.; ∴ 4 yd. = 4 × 3 ft.
> means is greater than; thus 5>2 and
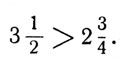
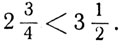
≈ means is approximately equal to; thus

≠ means is not equal to; thus, if x=5 and у = 2, x ≠ y.
Examples:
1. 32> 3 is read 32 is greater than 3.
2. N = 8 is read N is equal to 8.
3. (½)2< ½ is read is less than .
4. Z ≠ 0 is read Z is not equal to nought.
5. π is read an approximation for π is
| 22 | . |
| 7 |
6. 2N = 14 ∴ N = 7 is read twice N equals fourteen, therefore N equals seven.
Meaning of Brackets
The contents of a bracket may be regarded as equivalent to a single number.
Thus (7 +3) means the number obtained by adding 3 to 7; and (N + 5) means the number obtained by adding 5 to N.
The product of 9 and (7 + 3) is written 9 (7 + 3).
The product of 9 and (N + 5) is written 9 (N + 5).
Similarly (p - q) : 7 means subtract q from p and divide the result by 7. It is usually written:
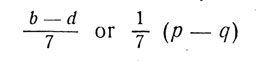
Also just as a2 means a • a, so (x + 4)2 means add у to x and multiply the result by itself. Brackets show the order in which operations must be performed.
Thus, 5 + 2(3 + 4) means add 4 to 3, double the sum, add the result to 5.
5 + 2(3 + 4) = 5 + 2 × 7 = 5 + 14 = 19.
But (5 + 2)3 + 4 means add 2 to 5, multiply the sum by 3, add 4 to the result.
(5 + 2) • 3 + 4 = 7 × 3 + 4 = 21 + 4 = 25.
And (5 + 2) • (3 + 4) means, add 2 to 5, add 4 to 3, multiply the first sum by the second sum.
(5 + 2) • (3 + 4) =7 × 7 = 49.
Thus, if an expression in brackets is multiplied by a number, each term in the brackets must be multiplied by that number, when the brackets are removed.
area площадь
bracket скобка
deal with иметь дело с
depth глубина
depth of an element высота элемента
ft. = foot фут (30,5 см)
formula формула
length длина
rectangle прямоугольник
relation соотношение, отношение
stand for символизировать, означать
width ширина
yd. = yard ярд (914,4 мм)
Addition and Subtraction of Positive and Negative Numbers
The addition of the two positive numbers +3 and +4 gives the sum +7.
To add two negative numbers such as -3 and -5 with the help of the number scale we count down 3, and starting from -3 we count down 5; the sum is -8.
The absolute value of any number is obtained by disregarding the sign of the number. Thus +5 and -5 have the same absolute value, 5.
A rule for finding the 'sum of any two numbers which have like signs may now be stated: to add any two numbers having like signs, find the sum of the absolute values and prefix the common sign.
The sum of + 6 and - 4 is + 2, and that of - 5 and + 2 is - 3. This suggests the following rule for finding the sum of two numbers having unlike signs: to add any two numbers having unlike signs, find the difference of the absolute values and prefix the sign of the greater.
Frequently the numbers to be added are horizontally arranged. They are to be added mentally without copying them in columns.
1. + 7, - 2
2. - 2w, - 4w
3. 13xy-20xy
4. r - 4r
Observe that sometimes the plus sign is not written when the first number given is positive.
When there are several numbers to be added, some of them positive, some negative, it is a principle of the order of operations that the numbers may be added in any order. It is. usually most convenient first to add the positive numbers, then to add all the negative numbers, and finally to combine the two results.
Example:
Add + 7, - 3, + 5, - 8.
Solution: 7 - 3 + 5 - 8 = 7 + 5 - 3 - 8 = 12 - 11 - 1 Ans.
In practice we do not actually rewrite the numbers in a changed order, but merely add them in that order mentally.
When the numbers to be added are not all of the same kind, we usually arrange in columns, as in arithmetic. We must make sure that all the terms in each column are like terms, differing only in their numerical coefficients.
Example:
Add 2f + 4i; 3f + 2i; and 4f + 3i.
2f+4i 3f+2i + 4f+3i 9f+9i
An example such as 7 - 5 may be considered as the subtraction of 5 from 7 or as the addition of - 5 to 7. The subtraction of any number is equivalent to the addition of a number having the same absolute value but the opposite sign. The subtraction of - 4 from + 6 gives the same result as the addition of - 4 to + 6. A rule for subtraction is therefore: change the sign of each term of the subtrahend and add. Do not change the sign in the work on your paper, but change it mentally.
When the minuend or subtrahend contains more than one term, the work is arranged in columns of like terms, as it was for addition.
Example: Subtract 4b - 2 from 5b + 3.
Solution:
Minuend 5b + 3
Subtrahend 4b - 2
Difference b + 5
Check, when b = 1;

The Product of a Positive and a Negative Number
According to our study of the order of operations a × b gives the same product as b × a. What, therefore, is the product of - 13 and + 2?; of - 3b and + 5?
Multiplication and Division
The product of a positive number and a negative number in each of the above instances is negative. More briefly - the product of any two numbers with unlike signs is negative.
If by addition we seek to find the product of 2a2 - ab - 5b2 by 3, we write the multiplicand three times:
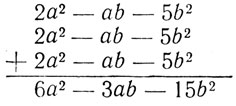
∴ 3(2a2 - ab - 5b2) = 6a2 - 3ab - 15b2Ans.
Notice that in the answer each term of 2a2 - ab - 5b2 has been multiplied by 3:
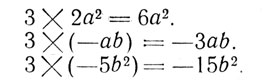
When a polynomial is multiplied by a monomial, therefore each term of the polynomial is multiplied in turn by the monomial.
We have learned that the product of two negative numbers is a positive number. Since the product of two positive numbers is also a positive number we may say briefly that the product of any two numbers with like signs is positive.
Division
When dividing two numbers that have like signs, the quotient is positive; when dividing two numbers that have unlike signs, the quotient is negative.
It is interesting to note the close relation between division and multiplication. Any question in division may be stated in the language of multiplication, just as any question in subtraction may be stated in the language of addition.
Division may be indicated by words, by the division sign :, or by a fraction. The numerator of the fraction is the dividend, and the denominator is the divisor. The three examples: 12x : 3; divide 12x by 3; and
| 12x |
| 3 |
have the same meaning and the same result, 4x.
Division examples may be proved by multiplication, or by numerical substitution.
like signs подобные знаки
monomial одночлен
polynomial многочлен
positive and negative numbers положительные и отрицательные числа
unlike signs знаки «плюс» и «минус»
Products and Powers
When two or more numbers are multiplied together, the result is called the product.
In algebra the product of two numbers X and У may be written in any of the forms X × Y, У × Y; X·Y, Y·X, XY or YX. The form XY is the most usual. Similarly the product of X, Y and Z may be written XYZ or XZY or YXZ or ZXY or ZYX, but it is usual to write the factors in alphabetical order, i. e. XYZ.
The beginner should note carefully that this differs considerably from the usage in arithmetic. In arithmetic the product of 4 and 5 is written 4 × 5 or 4·5, but not 45, which means 4 × 10 +5. The pupil should also note carefully the difference between 2 × 3 × X and 23X. The former means 2 × 3 × X, the latter means twenty-three times X.
When symbols are multiplied by a number, the number is usually placed before the symbols, with no sign of multiplication between. Thus 7pq means 7 times the product of p and q, or 7 × p × q. Also 253XYZ means 253 times the product of X, Y and Z, or 253 × X × Y × Z.
Each of the quantities multiplied together to form a product is called a factor of the product. Thus 3, 5, p, q are the factors of the product 15 pq.
When one of the factors of a product is a numerical quantity, it is called the coefficient or the numerical coefficient of the remaining factors.
Thus in the product 7 pq, 7 is the coefficient of pq. Similarly in the product 24abc, 24 is the coefficient of abc. It is sometimes convenient to consider any factor or factors, of a product as the coefficient of the remaining factors. Thus, in the product 7pq, 7p is the coefficient of q or 7q is the coefficient of p. A coefficient which involves letters is called a literal coefficient.
When the coefficient is unity, it is usually omitted. Thus we do not write Ix, but simply x.
The product obtained by multiplying together several factors all equal to the same number is called a power of that number. Thus 3 × 3 is called the second power (or square) of 3; 5 × 5 × 5 is called the third power (or cube) of 5; X × X × X × X × X is called the fifth power of X, and so on.
The following notation is used 3 × 3 = З2; 5 × 5 × 5 = 53; X × X × X × X × X = X5 and the small figure which indicates the number of equal factors is called the index of the power.
Thus in 42, 73, x5, the indices are 2, 3, 5 respectively. 32 is usually read 3 squared; 53 is read 5 cubed; X5 is read X to the fifth; and so on.
The first power of a number is the number itself. We do not usually write X1 but simply X. Thus X, 1X, X1, 1X1, all have the same meaning. It should be noted that every power of 1 is 1.
The pupil must distinguish between coefficient and index.
Fractional coefficients which are greater than unity are usually kept in the form of improper fractions. Thus
| 10 | xy |
| 7 |
is written more frequently than
| 1 | 3 | xy |
| 7 |
If one factor of a product is equal to 0, the product must equal 0, whatever values the other factors have. It follows that every power of 0 is 0. A factor 0 is usually called a zero factor.
Any collection of numbers and symbols connected by the signs +, −, × , : is called an algebraic expression.
Parts of an expression separated by the signs + or - are called terms. The signs X and : do not separate terms.
Thus 3а + 4c × p - 7× + qr + s : 2t is an expression of five terms. It should be noted that 4c?p is a single term. So are qr and s : 2t.
When no sign precedes a term, the sign + is understood.
An expression which consists of one term, e. g. 8b is called a simple (or monomial) expression. An expression which consists of two or more terms is called a compound expression. An expression of two terms, as 3c - 4d is called a binomial expression; one of three terms, as 3x + 4y - 2z, a trinominal; one of more than three terms a multinomial or polynomial.
A term which consists of the product of a number of letters or numbers, so that only multiplication and neither addition nor subtraction nor division occurs, is called an integral term. An expression containing a number of integral terms separated only by the signs f and - is called an integral algebraic expression.
An expression in which the letters occur under a root sign
___ 3___
(e. g., √ x, √ху )
is called an irrational expression. If the letters do not occur under a root sign, the expression is called rational. We shall be chiefly concerned with expressions which are both rational and integral.
In the case of expressions which contain more than one term, each term can be dealt with by the rules already given, and by combining the terms the numerical value of the whole expression is obtained. When brackets are used, they have the same meaning as in arithmetic, indicating that the terms enclosed within them are to be considered as one quantity.
|
ПОИСК:
|
© GENLING.RU, 2001-2021
При использовании материалов сайта активная ссылка обязательна:
http://genling.ru/ 'Общее языкознание'
При использовании материалов сайта активная ссылка обязательна:
http://genling.ru/ 'Общее языкознание'