
FRACTIONS
A fraction is a part of unit, such as ½, ¾ etc.
A fraction has a numerator and denominator.
Example: in the fraction ¾ -3 is the numerator, and 4 is he denominator.
In the fraction the numerator is being divided by the denominator.
The fraction
| 2 | ||
| 7 |
indicates that 2 is being divided by 7.
A mixed number is an integer together with a fraction, such as etc. The integer is the integral part, and the fraction is the fractional part.
An improper fraction is one in which the numerator is greater than the denominator, such as
| 2 | 3 | |
| 5 |
| 7 | 3 | |
| 8 |
etc.
To change a mixed number to an improper fraction:
a) Multiply the denominator of the fraction by the integer.
b) Add the numerator to this product.
c) Place the sum over the denominator of the fraction.
Example: Change
| 3 | 4 |
| 7 |
to a fraction. Solution:
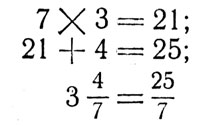
Addition of Fractions
Fractions cannot be added unless the denominators are all the same. If they are, add all the numerators and place this sum over the common denominator.
Add up the integers, if any.
If the denominators are not the same, the fractions in order to be added must be converted to fractions, having the same denominators. In order to do this it is first necessary to find Lowest Common Denominator (L. С. D.). The L. C. D. is the lowest number which can be divided by all the given denominators. Example: the L. C. D. of ½
| 1 |
| 3 |
and
| 1 |
| 5 |
is 2 × 3 ×5 = 30.
Subtraction of Fractions
More than two numbers may be added at the same time. In subtraction, however, only two numbers are involved. In subtraction, as in addition, the denominators must be the same. One must be careful to determine which term is first. The second term is always subtracted from the first, which should be of a larger quantity.
To subtract fractions: a) Change the mixed numbers, if any, to improper fractions.
b) Find the L. C. D.
c) Change both fractions to fractions having the L. C. D. as the denominator.
d) Subtract the numerator of the second fraction from the numerator of the first, and place this difference over the L. C. D.
e) Reduce if possible.
Multiplication of Fractions
To be multiplied, fractions need not have the same denominator.
To multiply fractions:
a) Change the mixed numbers, if any, to improper fractions.
b) Multiply all the numerators and place this product over the product of denominators.
c) Reduce if possible.
Illustration: Multiply
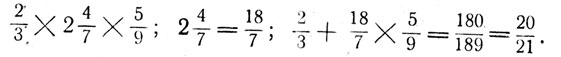
Division of Fractions
In division as in subtraction only two terms are involved. It is very important to determine which term is first.
If the problem reads
| 2 |
| 3 |
divided by 5, then
| 2 |
| 3 |
is the first term and 5 is the second. If it reads "How many times is
| 1 |
| 2 |
contained in
| 1 | ?" | |
| 3 |
then is first and
| 1 |
| 2 |
is second.
To divide fractions:
a) Change the mixed numbers, if any, to improper fractions.
b) Invert the second fraction and multiply.
c) Reduce if possible.
Illustration: Divide
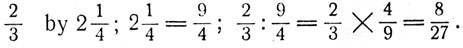
A mixed fraction has a fraction as the numerator, or as the denominator, or as both.
common denominator общий знаменатель
convert превращать
fraction дробь
fractional дробный
if any если имеется, если есть
improper fraction неправильная дробь
integer целое число
integral целый
invert обращать, менять порядок, переставлять
Lowest Common Denominator (L.C.D.) общий наименьший знаменатель
mixed number смешанное число
numerator числитель
place over помещать над
quantity величина, количество
reduce сокращать, преобразовывать
solution решение
Addition and Subtraction of Decimal Fractions
The addition and subtraction of decimal fractions is performed in the same manner as the addition and subtraction of whole numbers.
1. When we add two or several decimal fractions, all of these numbers should have the same number of places to the right of the decimal point.
2. If we subtract one decimal fraction from another, the two should have the same number of places to the right of the decimal point.
3. We shall refer to places to the right of the decimal point as decimal places.
In a set of addends or in a minuend or subtrahend, one or several of the numbers may have more decimal places than the others. In such situations we note the number having the fewest decimal places and discard the digits which are to the right of these decimal places in the other numbers. For example, in adding
45.6723 156.78
we discard the digits 2 and 3. But we do not simply ignore these discarded digits. They may cause a change in one of the digits we intend to use. If we have
45.6723 156.7
We must rewrite it as:
45.7 156.7
according to the following rule:
If the first digit (figure) at left of the portion that is to be discarded is either 0, 1, 2, 3 or 4, then the last digit on the right that is to be retained should be left unchanged. If the first digit (figure) at the left of the portion that is to be discarded is either 5, 6, 7, 8 or 9, then the last digit on the right that is to be retained should be increased by 1.
Such discarding of the unnecessary decimal places is known as the rounding of numbers.
When 45.6723 was rounded to one decimal place, that is to tenths, we obtained 45.7 because the first digit of the discarded portion was 7, and, therefore, the last digit on the right (the 6) was increased by 1, and we thus obtained 7.
The actual addition and subtraction of decimal fractions is performed in the same manner as in the case of the whole numbers so that decimal points are all in a vertical column as shown below:
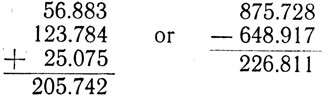
Multiplication of Decimal Fractions
The only difference between the multiplication of whole numbers and decimal fraction numbers is that we must take into consideration that some portion of one or both factors is fractional, as indicated by the decimal points.
Now, instead of multiplying decimal fractions let us multiply whole numbers 3,672 and 275. To obtain 3,672 from 3.672 we move the decimal point 3 places to the right, that is we multiply the number by 1,000 and to obtain 275 from 2.75 we move the decimal point two places to the right, that is we multiply it by 100. - Thus, the product 3,672 × 275 is 1,000 × 100= 100.000, times the product 3.672 × 2.75.
When the product of the whole numbers 3,672 × 275 is obtained, we must divide it by 100,000 that is, move the decimal point 5 places to the left. The multiplication of the whole numbers is:

The decimal point (not written) is at present on the extreme right of the product, that is, we have 1,009,800 and after moving it 5 places to the left we have 10.098.
Notice that one factor has 3 decimal places, and the second factor has 2 decimal places. The product has 5 decimal places, that is: the number of the decimal places in the product is equal to total number of decimal places in the factors.
Division of Decimal Fractions
The only difference between the division of whole numbers and that of numbers containing decimal fractions is that we must take into consideration the fact that some portion of either the dividend or the divisor, or of both is fractional, as indicated by the decimal points.
Furthermore, when we performed division with whole numbers, we often could not complete this operation as we obtained a remainder. Thus, we have before us two questions:
1. Where shall we locate the decimal point in the quotient?
2. What shall we do in the case of a remainder? We examined the effect of the moving of the decimal point.
Let us apply the obtained results to the process of division. Let us first examine the division of a decimal fraction by a whole number, for example: 111.78:9. We shall proceed as in the division of whole numbers
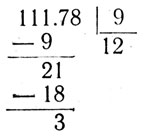
Note, that the division of the whole part leaves a remainder 3, and that we have a fractional part 0.78, that is, we are left with 3.78. From this point on we can't expect anything else but some fraction in the quotient, if we continue the division. If now we bring down the next digit, that is 7, we shall have 3.7 or 370 tenths. If we divide 37 tenths by 9, we shall have a certain number of tenths in the quotient. We shall, therefore, place a decimal point after the 2 in the obtained quotient and continue the division as usual. We have then:

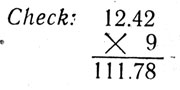
Thus, we observe that the division of a decimal fraction by a whole number is performed in the same manner as the division of a whole number by a whole number.
The whole part of the decimal fraction will give the whole part of the quotient. As soon as we bring down the first digit from the decimal part of the dividend, we shall begin to obtain the decimal part (the fractional part) of the quotient. This procedure always serves for the division of decimal numbers by whole numbers.
Now we shall apply the results just obtained to the division of decimal fractions by decimal fractions. Let us perform the division 176.28:2.6.
We know that the multiplication of the dividend and of the divisor by the same number does not produce any change in the quotient. When we multiply the dividend by some number, the quotient is multiplied by the same number, but when we multiply the divisor by some number, the quotient is divided by the same number. This fact enables us to change the dividend 2.6 into a whole number. This change is accomplished by moving both "decimal points one place to the right; thus, both the divisor and dividend are multiplied by 10. The divisor 2.6 becomes 26, and dividend 176.28 becomes 1,762.8.
Quotients with Repeated Decimals
Very often the division of numbers, whole numbers or numbers with decimal fractions, cannot be completed to give an exact result. At some stage of the division we reach a situation where the quotient or a part of the quotient repeats itself, and thus the division may be carried on indefinitely. In all such cases, however, an exact quotient cannot be obtained. In such situations the process of division must be stopped at some place.
Often the point where the division stops is determined in the statement of the problem.
The following example will illustrate the repeating:
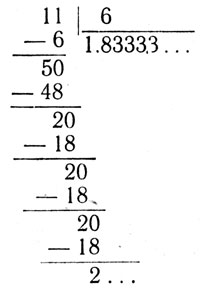
Note that during the division above, we brought down zeroes whenever we wished to continue the process. All these zeroes assumedly come from the places to the right of the decimal point. We note that the quotient 11:6 = - 1.83333... may contain as many repeated 3's as we wish. However, if we decide to stop, less than 5, we merely drop the digits that are beyond the place where we wish to stop.
bring down зд. сносить
decimal fraction десятичная дробь
decimal place десятичный разряд
decimal point запятая в десятичном числе
digit цифра, однозначное число, разряд
discard отбрасывать
locate определять место, назначать место
portion часть, доля
remainder остаток
repeated decimal повторное десятичное число
that is to be discarded который должен быть отброшен
vertical column вертикальный столбик
Examples of False Arguments
I. 45 - 45 = 45.
Someone stubbornly asserted that 45 - 45 = 45.
In support of this, he argued thus:
We write the subtrahend in the form of a sum of the consecutive natural numbers from 1 to 9 and the minuend in the form of the sum of the same numbers, but we take them in the opposite order (from 9 to 1). 20
Locating the subtrahend under the minuend:
1) 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2+1;
2) 1+2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.
Now we calculate the difference. With this aim we successively subtract the numbers of the second line from the numbers on the first line, beginning by subtracting the 9. Since 9 cannot be subtracted from 1, we take a unit from the two, we have: 11 - 9 = 2. In a similar way we obtain the differences of the number 11 and 8, 12 and 7, 13 and 6, 14 and 5 respectively, and 3, 5, 7 and 9. Carrying out the subtractions of four from five, three from seven, two from eight, and finally one from nine, we obtain the following results: 1, 4, 6, 8.
Thus:
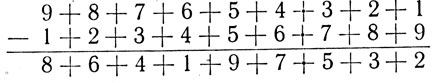
It is not hard to establish, that
8 + 6+ 4+1+9 + 7 + 5 + 3 + 2 = 45.
Thus 45 - 45 = 45.
II. 40 : 8 = 41.
Little Peter did not like to calculate mentally. When he wanted to divide 40 nuts equally among 8 boys, he wrote the division.
When he carried out the division, it looked thus:
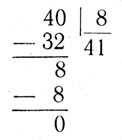
The answer worried Peter. He understood very well that each of the boys cannot obtain more nuts than their total number, but he could not discover his mistake in the division.
Help little Peter to understand his mistake.
III. Two times two is five. We shall take the following equality: 4 : 4 = 5 : 5.
When we take out the common factor from each member of the equality (1), we have:
1) 4 × (1:1)=5 × (1:1) or
2) (2 × 2) × (1:1) = 5 × (1:1)
Finally, knowing that 1:1 = 1, from relation (2) we establish:
3) 2 × 2 = 5
IV. Is there a proportionality here?
Let us consider a few problems together with their answers obtained as a result of applying the simple rule of three.
1. An aeroplane has climbed to an altitude of 8 km. in 32 min. To what altitude will it climb in four hours?
Answer:
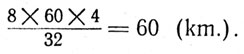
2. A motor of h. p. installed on a boat gives the boat a speed of 8 km/hr. What speed is given to the same boat by a 10 h. p. motor?
Answer:

V. What will a yearly growth of 40 per cent give in five years?
According to the five-year plan a certain company should increase its production threefold. During the first three years it increased its productivity by 30 per cent yearly (as compared with the preceding year). Is it fulfilling the task of its five-year plan or not?
We recall that productivity of an enterprise is the quantity of production for some definite period of time, for example per day (daily productivity). If one takes the productivity at the beginning of the five-year plan as 100 per cent, then (for a three-fold increase during the five-year period) at the end of the five-year period the productivity should become equal to 300 per cent, i. e. increase by 200 per cent. With such an increase of productivity for the five-year period, for one year it should obtain an increase 5 - 40 per cent. Consequently in undergoing a yearly growth of 30 per cent it is not fulfilling its five-year plan.
However this conclusion is quite incorrect. In the argument there is a flaw. Find it.
VI. A new rule for multiplying fractions.
A student disclosed to his mathematics teacher: “I have found a new rule for multiplying mixed fractions, much simpler and easier to apply than the one which you have explained to us and the one described in textbooks. The point is that in adding mixed fractions one has to add separately the integers and separately the fractions. For example:
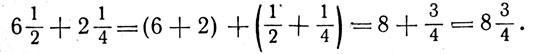
The same is done also in subtraction: from integers we subtract the integers, from the fractions - the fractions:
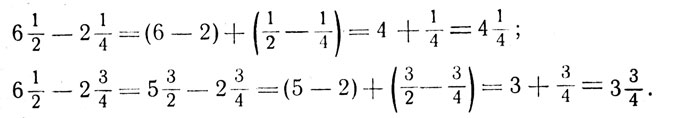
Obviously one should proceed also in the same way in multiplying mixed fractions: the integer should be multiplied by the integer and the fraction by the fraction, for example:
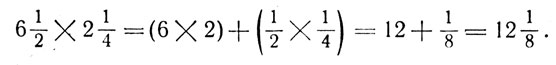
My rule is simpler to apply and easier to understand than yours. What did you think of it?”
VII. What happened to the dollar? In a box there were two baskets of pears, 150 in each. The price of the pears was determined in the following way: from the first basket the pears are sold at one dollar for ten, and from the second basket at a dollar for fifteen. Thus, for all the pears from the first basket the amount received was 150:10=15 (dollars), for all the pears from the second basket 150:15-10 (dollars), and in all 25 dollars.
The seller thought that by taking from the first basket ten pears and from the second basket fifteen he will sell 25 pears for 2 dollars. Therefore he mixed the pears from both baskets together and sold the 150 × 2 - 300 (pears) at 2 dollars for 25. As a result he received 2 × (300 : 25) - 24 (dollars), i. e. one dollar less than the expected sum of the receipts.
What happened to the dollar?
VIII. A Father's Will.
According to the will of their father three sons were to divide among themselves a herd of seven horses in such a way that the eldest was to receive one half of the herd, the middle one - one fourth, and the youngest - one eighth.
The father's will worried his heirs considerably.
However, a way was found out of the difficult situation. An old neighbour added his own horse to the herd undergoing division and to the satisfaction of the brothers proceeded with the division.
As a result of it, the eldest son received four horses, the middle one - two, and the youngest - one. The neighbour's horse, not needed any longer, was gratefully returned to its clever owner. Thus it turns out that father's will can be solved in integers.
Is it so?
IX. 2 × 3 = 4.
Somebody decided to demonstrate that 3 times 2 makes not 6 but 4. In carrying out this strange venture, he took in hand an ordinary match and asked those present to follow carefully the process of this thought.
“By breaking the match in halves”, stated the strange mathematician, “we shall have two. Doing the same to one of the halves we shall have a second time two. Finally, carrying out the same operation on the second one of the halves, we shall obtain a third time two. Thus, taking three times two we have obtained four and not six, as one is accustomed to think”.
h. p. = horse power лошадиная сила
i. e. = that is т. е.
in all всего
is accustomed to think привык думать
it turns out получается
km/hr. = kilometre per hour км/час
threefold в три раза, утроенный
two times two дважды два
will зд. воля, завещание
|
ПОИСК:
|
© GENLING.RU, 2001-2021
При использовании материалов сайта активная ссылка обязательна:
http://genling.ru/ 'Общее языкознание'
При использовании материалов сайта активная ссылка обязательна:
http://genling.ru/ 'Общее языкознание'