Глава I. Понятие о документной лингвистике

Взаимосвязь естественного и искусственного языков

В связи с обработкой документов машинным способом особенно важной и актуальной стала задача перевода документов на язык машины. Машина требует принципиально нового подхода к языку. Ей необходим язык формализованный, представляющий собой какую-либо знаковую систему, с помощью которой можно точно и конкретно передать любые сведения.

В структуре любого языка могут быть выделены четыре основных уровня: набор основных символов, слова, выражения (понятия), предложения.

Основные символы языка - это неделимые знаки, с помощью которых строятся слова. Слова - это наименьшие смысловые единицы языка, образующиеся путем соответствующего расположения символов. Из слов образуются выражения (понятия) и из выражений - предложения. В русском языке набором основных символов является алфавит, состоящий из 36 букв, и знаки пунктуации.

Существуют три типа естественных языков, отличающиеся количеством основных символов, семантикой и синтаксисом:

первый тип языков, в которых каждое слово обозначается специальным символом, например, китайский язык, где общее число символов составляет около 100 000;

второй тип, у которых отдельные слоги обозначаются своими символами, общее число символов при этом составляет около 30 000;

третий тип - языки, имеющие определенные алфавиты букв, из которых образуются слоги и слова, общее число букв составляет порядка 30.

Практически применяются языки смешанных типов. Например, математический язык включает язык третьего и первого типов. Первый тип - язык формул, где отдельные символы обозначают целые слова (например, + сложение, X умножение). Если машинный язык рассматривать применительно к этим трем типам, то следует отнести его к языку первого типа, где определенные символы - коды операций - означают выполнение определенных действий. Например, в машинном языке для машины "Урал-2" набор символов 01а означает сложение с числом, находящимся в ячейке памяти с адресом "а".

При сравнении естественного и искусственного языков наблюдаются следующие параллели:

Естественный язык по отношению к искусственному характеризуется избыточностью информации. Каждое слово, а иногда и целое понятие, можно выразить одним символом. Например, слово "серебро" - Ag; выражение "отношение" длины окружности к диаметру - π.

В первом случае слово "серебро" может обозначать металл, ювелирное изделие, столовый прибор; во втором - Ag - конкретное значение; в третьем - понятие выражается тридцатью тремя буквами; в четвертом - одной буквой.

Естественный язык стихийно развивался на основе ассоциативного мышления. Поэтому каждый лингвистический знак представляет перечисление многих ассоциаций, которые формируются (определяются) смыслом, содержанием. Смысловые контакты имеют логическую, эмоциональную и эстетическую природу. Ассоциативные возможности человеческого мозга ничем не лимитированы. Поэтому для каждого лингвистического знака существуют ничем не ограниченные возможности стать носителем новых ассоциаций. Это свойство знака служит источником метафоричности естественного языка.

Искусственно созданные формализованные языки математики строятся на основе логического анализа, при котором выделяется некоторое минимальное число первичных, неопределяемых понятий, а все остальные определяются через первичные. Примером такого языка является символический язык математической логики. Словарь такого языка состоит из исходных, неразложимых символов, каждому из которых однозначно соотнесен некоторый математический объект или операция. Из исходных символов составляются конечные последовательности, называемые формулами.

Символы и формулы выступают в качестве однозначных математических знаков. Полностью исключаются субъективные интерпретации математических знаков. В математике не допускаются также ассоциации эстетического и эмоционального характера или сближения знаков по их форме. Человеку, знакомому с языком математики, никогда не придет в голову каким-либо образом ассоциировать знак умножения X с близким ему по форме знаком переменной X. Из правильно построенных формул, выступающих в роли посылок, выводятся заключения. В ходе этого выведения широко используется эквивалентность (синонимия) математических знаков и выражений.

У знака математического метафоричность полностью отсутствует. Математический язык строит свои выводы и заключения на широкой эквивалентности между отдельными математическими знаками.

Естественный язык воспринимается и используется человеком в значительной своей части интуитивно. Всякий математический язык существует и функционирует в виде логического построения, каждый элемент имеет осознанную значимость. Следовательно, с одной стороны, лингвистический знак оказывается семантически богаче математического знака. С другой стороны, однозначность математического языка позволяет недвусмысленно и исчерпывающе формулировать задачу, решать ее алгоритмическим путем, т. е. путем точного предписания и выполнения в определенном порядке некоторой системы операций.

Так как математический знак однозначен, а лингвистический знак имеет сложную логическую, экспрессивную и даже эстетическую структуру, то математическая интерпретация понятия связана с расчленением лингвистического объекта и выделением в нем одного или несколько логико-смысловых или формальных компонентов. Остальные логические и формальные элементы лингвистического объекта, а также экспрессивно-эстетические оттенки из рассмотрения исключаются.

Таким образом, применение математических методов в языкознании имеет своей целью заменить интуитивно сформированную лингвистическую задачу одной или несколькими более простыми, логически сформулированными и имеющими алгоритмическое решение математическими задачами. Такое расчленение сложной лингвистической проблемы на более простые алгоритмизуемые задачи называется математической экспликацией лингвистического объекта. Математическая экспликация обязательна в том случае, если для решения лингвистических задач, например, для перевода или реферирования текста используется электронно-вычислительная машина (ЭВМ). Однако всякая математическая экспликация имеет свою оборотную сторону. Сосредоточивая внимание на одних сторонах лингвистического объекта и отвлекаясь от других, математическая экспликация неизбежно дает схематизированную и обедненную картину лингвистического явления. Перевод текста, выполненный ЭВМ с помощью формализованного языка, - в лучшем случае логическая канва текста, лишенная смысловых оттенков и экспрессивных окрасок оригинала. Поэтому каждую математическую экспликацию следует рассматривать не как закон, а как математический аналог лишь одной из существенных сторон для данного исследования. Математический аналог выступает в роли модели лингвистического объекта. Каждая из моделей описывает определенную сторону лингвистического объекта. Сумма таких моделей может дать исчерпывающее описание объекта. Метод моделей принято называть моделированием, он становится сейчас основным методом познания для многих наук. Общее отличие языка естественного от искусственного - большая структурная сложность. Выявление минимального словаря, его описание при переводе текста с естественного языка на искусственный является серьезной проблемой. Однако есть возможность решать эту проблему по частям, последовательно двигаясь от простого к сложному. Для этого нужно учесть факт "вложенности" одних фрагментов языка в другие. Сначала выделить и подвергнуть формализации сравнительно простой фрагмент языка и затем последовательно наращивать полученную систему за счет расширения минимального словаря и добавления новых понятий.

Семантическая структура языка в целом схематично может быть представлена рядом вложенных друг в друга кругов, из которых каждый последующий круг включает предыдущий (рис. 1).

В большинстве случаев задание машине возникает у человека на естественном языке. Поэтому встал вопрос о расширении семантической функции ЭВМ с тем, чтобы она могла переработать информацию, записанную на естественном языке. Семантическую функцию ЭВМ нельзя расширить за счет введения в машину всего естественного языка, так как естественный язык сложен, а память ЭВМ ограничена. Появилась необходимость создать сокращенный базовый язык, который включал бы наиболее важные (часто употребляемые и информационно нагруженные) единицы языка.

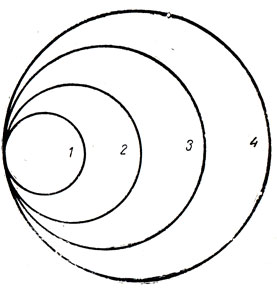
Рис. 1. Схема семантической структуры языка

Единицы базового языка отбираются путем изучения естественного языка с помощью приемов теорий вероятности и математической статистики. При этом исследуется не весь язык, а некоторый подъязык - совокупность языковых элементов и их отношений в текстах с ограниченной тематикой.

При этом выделяются две задачи:

отбор наиболее важных единиц подъязыка и определение их информационных характеристик;

построение правил, связывающих форму выделенных единиц с их содержанием.

Таким образом, первое включает выделение наиболее часто употребляемых слов, словосочетаний, грамматических конструкций, определение структуры слова, распределение информационной нагрузки в нем. Иными словами, на первом этапе строится морфология и лексика базового языка. В процессе решения второй задачи отыскиваются правила сочетаемости слов и классов слов (синтаксис), а также правила различия омонимии лингвистических единиц.

Степень приближения к решению заданной задачи будет зависеть не только от того, насколько корректно будут выбраны входящие в базовый язык единицы, но также и от быстроты создания этого языка и от времени, в течение которого он без изменений будет использоваться в системе "человек - машина".